Betting 101
Level 1 - NGMI
Welcome Avatar!
The idea is that this Betting101-post shall contain all the necessary information to get started in the betting world. Therefore, in order for it to be an introduction of highest quality, it will be continually updated as new thoughts and questions emerge. If you are a novice, prior to asking questions in future Q&A’s it is highly recommended to reread this post since there is a fair chance the answers are provided here.
What is betting?
Betting is in its simplest form a wager of money on an uncertain event taking place in the future. The choice of underlying event is arbitrary, as long as there is a sample space containing more than one possible outcome the necessary conditions for betting to come about are basically fulfilled.
The most popular kind of betting is on events containing disjoint/mutually exclusive outcomes owing to the simplicity of standardization of these types of betting products. A majority of sports betting and horse racing wagering falls into this category.
“Disjoint/mutually exclusive outcomes”: Disjoint/mutually outcomes cannot coexist, *either* team A wins *or* team B wins. *Either* horse C wins *or* another horse wins.
“Standardization”: Developing clear rules that can be reapplied to all similar future events, hence simplifying *a lot* for all market participants. Compare with e.g. standardization of commodities for trading purposes.
Fundamental betting terms
To simplify the further discussion on this substack we begin by extending your betting vocabulary with a few very fundamental concepts. These will reappear basically everywhere and if you are not feeling completely comfortable with them after the next few paragraphs, don’t worry, it won’t be long until you are.
Odds
Essentially a number providing information about the size of a possible payoff. There are a number of ways to represent this payoff structure but due to its simplicity we will solely use decimal odds. If you favor Russia to beat Ukraine in a game of hockey and a bookie offers 1.14 on Russia to win, you simply multiply your stake by 1.14 to find out how much money will be returned on your wager in the case of it winning. The net winnings are then obtained by subtracting the size of your wager.
Note: If you are used to other odds representations such as the american or the fractional versions, there are a number of odds converters online to use. A better option is however to simply get used to them all, Wikipedia has a great explainer on the relationship between them and after reading that combined with having a few exposures you will perform the conversions easily in your head.
Probability
A term basically everyone is familiar with, yet something that can cause confusion and pose interesting philosophical questions as one delves deeper and considers more than the most basic notions. For practical betting purposes, simply think of iterating an event over and over again while observing how often a given outcome occurs. The probability of the outcome of interest is then defined as the fraction
Autist note: The notion of “over and over again” is vague and deserves a thorough discussion. Our piece on bet sequences contains the basics of probabilistic convergence.
Implied probability
Imagine a horse race with no track take. As the race is off and the betting closes the public has implicitly assigned each horse an exact win probability, calculated by computing the multiplicative inverse of the decimal odds corresponding to the horse of interest. This implied probability is of utmost importance. If you for some reason hold divergent opinions and your estimated probability exceeds the implied one by the odds then *given your analysis* there is an opportunity in the market. Why? Purely because you have found a +EV case! What is EV? Keep reading!
Under real circumstances (betting exchanges excluded) there is a fee baked into the odds, hence the odds must be adjusted prior to mapping them to probabilities if ones aim is to reverse engineer the bookie’s pricing. This adjustment may actually be quite involved at times and will not be something for us to look into for now.
For betting purposes the ordinary 1/ODDS is all that matters regardless of what fees/take apply. If we define this number to be the implied probability then a helpful description of the term would be:
Implied probability ~ “the necessary probability for a wager on an outcome to be profitable”.
Expected value [EV]
Suppose that you would face the same exact betting opportunity *many* times and bet exactly the same amount on each such occasion. Now, compute the average unit net profit/loss (normalize each profit/loss by dividing by the size of your stake) on each bet over this full sequence. This number, whatever it turns out to be, is known as the expected value of the bet. Mathematically, it is computed as
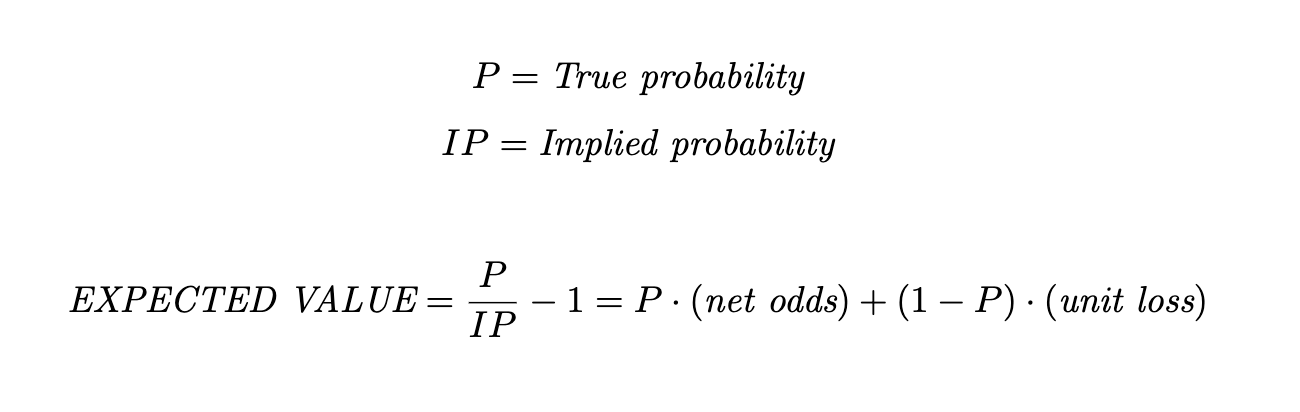
In practice, a great heuristic is to investigate all +EV openings further while always ignoring any -EV bets (possibly taking the other side). However, since it is often a difficult task to come up with true probabilities the expected value is in itself uncertain, hence EV is rarely providing an actionable, precise number. Nevertheless the way of looking at things from an EV point of view provides a great mental framework to value basically any wager.
Autist note: Even though it holds true in most cases, a +EV bet is not necessarily favorable, and a -EV is not necessarily unfavorable. There are actually very interesting exceptions to this “rule” that will be handled in more advanced posts.
Return on investment [ROI]
ROI is a widely used term in betting contexts and is simply defined as the net profit/loss divided by the total turnover over a specified betting period.
There is an interesting connection between the expected value and the ROI measure. If one views the expected value as an abstract concept handling “true” probabilities, the ROI measure is its practical counterpart, only taking a finite, often small, sample into consideration. However, as the number of bets increases one may expect the ROI to converge to the true EV of the betting sequence, making them both more or less equivalent. A more detailed discussion on this can be found in “Bet sequences, an analysis”.
Variance
Strictly speaking, variance is a clearly defined mathematical measure of dispersion. Hence the variance is a *number* holding information regarding the spread of data. If we loosen up this strict definition a little bit and instead view variance on a scale ranging from 'low' to 'high' rather than as a specific number, we arrive at what is meant by variance in betting circles. If your portfolio is taking huge swings all the time, then this is a sign of *high* variance. On the contrary, if you are continuously returning X +- 1 % per month it is a demonstration of *low* variance.
Autist note: High EV is often coupled with high variance (see crypto for example). Why? Imagine a new, fresh market taking its first baby steps. Each opportunity out there can be viewed as a pair (EV, variance). Suppose that two betting propositions offer a different EV but equivalent variance and have all other things equal (correlations etc.). Market participants, or at least those providing the bulk of the volume, will then choose the (higher EV, equal variance) pair, immediately putting buy pressure on this investment, hence lowering its EV. Likewise, if you have two pairs (fixed EV, high variance) and (fixed EV, low variance), the market will prefer the one with low variance (if leverage is available one could simply map the low variance into equivalent variance, effectively reconstructing the earlier case), again forcing the EV down until equilibrium is reached.
Now realise that every single second, the market is indeed a new, fresh market taking its first baby steps, and it does not take long before you see that this framework inarguably provides a satisfying way of observing the market.
Food for thought: What is the ‘correct’ relation between EV and variance? Furthermore, is such a ‘correct’ relation necessarily ‘correct’ for everyone?
Bonus rugging
A scheme taking advantage of the betting propositions offered by bookmakers targeted at new customers. Tailor-made for newcomers. Substack posts containing "BR" in its title are associated with bonus rugging and a full introduction to the concept can be read here.
Return to player [RTP]
RTP is a measure of the ‘fee’ applied to the specific market by the bookmaker. The RTP is equal to the ratio of wagered money returned to the winning bettors, hence the name. If the RTP is high, it means more money is distributed between the market participants and less kept by the bookmaker. Thus, all things equal, a higher RTP is preferable for you as a bettor.
Autist note: The condition of all things being equal is, unsurprisingly, rarely satisfied. Since markets with very favorable terms tend to attract more sophisticated bettors, it automatically becomes much harder to find an edge. Only considering RTP while choosing betting markets to participate in (in fact done by many) is nothing but naive first-level thinking.
BR-note: If however you are bonus rugging then you *should* choose markets solely based on RTP. When executing BR you are at each step hedging all your bets and are therefore *guaranteed* to pay exactly (1-RTP) in fees for each bet you place. Clearly (1-RTP) is decreasing (you are paying *less* fees) with increasing RTP.
Last note: In fact, the RTP could equivalently be defined as the fraction of the wager you keep by taking on a fully hedged position. If the RTP is above 1, you may therefore infer that there is an arbitrage (and a profitable, risk-free strategy) available in the given market.
Below we have listed three different formulas for computing the ‘return to player’ of a market. The first one computes it for a two-way market, the second one for a three-way market and then the last one is a generalization to the arbitrary case with n different outcomes.
Betting exchanges
A betting exchange is a platform that allows individuals to bet against each other instead of betting against a bookmaker or a traditional sportsbook. In a betting exchange model, users can both back (bet for) and lay (bet against) outcomes, meaning they can act both as a traditional bettor and as a bookmaker. The world’s largest and most popular betting exchange is Betfair. Famous competitors are Smarkets, Matchbook and Betdaq, all three doing their best to gain a larger market share.
When a user backs a selection, they are effectively placing a traditional bet on that selection to win. When a user lays a selection, they are instead taking on the role of a bookmaker, offering odds on the selection to other users. The user laying the selection wins if the selection does not win, and loses if the selection does win.
The exchange earns revenue by charging a commission on the winning bets placed by users. The commission rate varies across different exchanges and can be as low as 2% of the [net] winnings.
Example 1: You log into Betfair and bet $100 on Man Utd to win against Arsenal, odds 2.88. If your bet wins, your net profit is $188. Betfair keeps 2 % [$3.76] of those winnings and returns the remaining $184.24 to your betting balance. In other words, the “real” odds post fees is 2.8424.
Example 2: You log into Betfair and lay $100 on Man Utd to win against Arsenal, odds 2.90. If your bet wins [Man Utd does *NOT* win], your net profits are $100. Betfair keeps 2 % [$2] of those winnings and returns the remaining $98 to your betting balance.
If however Man Utd wins the game, you lose $190 since you’ve let another market participant bet $100 on Man Utd to win at 2.90.
Note: Laying an outcome is equivalent to betting on all the remaining outcomes. I.e. laying a fixed amount of dollars on Man Utd as in the example above is the same as betting “the right” amounts on both ‘Arsenal’ and ‘The Draw’.








