A Thought Or Two
Level 4 - WAGMI 2.0
Do you have a friend who likes betting and would like to sharpen his/her action? Help them on their path by sharing the BowTiedBettor Substack. Win and help win!
Welcome Avatar!
When we first set up the Substack, one of the primary reasons was to sharpen our action. & being forced to map those latent thoughts hidden in the back of our heads into well crafted explanations has indeed been a clever trick [as noted by many before us] to perfect our edges.
Don’t misinterpret this as us being against the act of letting thoughts exist without further inspection. Definitely not. To be fair, in 99 % of the cases the time spent on deeper knowledge for an arbitrary niche question will yield zero. Nada.
& there’s some magic removed when certain concepts are made into 'study material'. Love to have a thought hanging around for a while [or forever] until the time has come for it to be handled properly…
Warning: This post could come along as somewhat disorganized. Much of the content is a direct function of a late night thought process, a process that gets bored to death by organization. Love to read organized posts. Hate writing them. How lucky we don’t have to read our own posts! :)
Thought A [Market efficiency]
Seen a lot of brain dead arguments [mainly by data enjoyooors] 'supporting' market efficiency. Everywhere. All the time. Excellent example of how repetitive & boring people are in general [everyone parrots & circulates what others are saying & travels through knowledge, devoid of context].
So, what is market efficiency?
The market’s perceived ability to price objects according to their underlying, ‘true’ probabilities (if we allow for such an abstraction). Effectively creating an environment where all strategies should be equivalent [profit-wise]. So how would you go about proving market efficiency?
Two options:
Show that each outcome is perfectly priced by the market.
Prove that no matter the strategy employed, profit expectations remain the same.
Can either be shown in real life? Of course not. This yields our first insight: since in practice market efficiency cannot be proven, any attempt at such a proof must naturally fall apart. There is no escaping, there’s no place to hide. Might be hard to find, but somewhere there *must* be a crack in the argument. Your mission: find this crack & *see*.
All there can ever be is *beliefs* about market efficiency. & whose beliefs should you trust? The practictioner's. If you wonder whether a specific market is efficient, refuse to ask the confused but of course very certain ‘data scientist’ & try to find yourself an autist gambler betting the market on an everyday basis to answer the question instead.
Random note: the greatest advantage of building great mental models? Don’t have to waste time cleaning, reading & manipulating data. Who enjoys working with data anyway? 100 % the most boring part of any ‘research process’.
Thought B [Bayes, Bayes, Bayes]
We’ll return to market efficiency, but the path towards it will have to be somewhat roundabout. Enter thought B. Bayes. Have been said many times by the cartoon horse before: Bayes is incredibly powerful. Why? Learning how to think in conditionals & inverses opens the door to a new dimension. The Bayes Dimension. And how do you learn to do such a thing? By studying Bayes. We preach Bayes all the time & of course the mids don’t see why. With no room for abstraction, they look at the formula & conclude: “nothing special about that”. It’s *a framework*. *Not* a formula.
Ability to think in conditionals = accustomed to & can entertain “if, then”-scenarios, even in complex cases. An arbitrary example: a sentence like “what is the probability of Brazil winning the 2018 World Cup, given them winning it in 2022?” doesn’t cause any confusion [conditional probability on a probability space is time independent] whatsoever.
Ability to think in inverses = appreciates that to truly answer the question in one direction, one must in many cases understand the reverse one. If you’ve never thought about the probability of a market price, given a true, underlying probability, how can you infer the [in practice] more important answer: the probability of a true, underlying probability, given a certain market price?
Mixing these two abilities with a suitable generative [either theoretical or practical, doesn’t matter] model is what we really mean when we repeatedly shill Bayes. Some would claim it isn’t an optimal mental framework in order to *think with precision*. Some are wrong.
Bayes is #1.
Intelligence guaranteed to skyrocket when *getting it*.
Back to market efficiency
Every single day tons of people ask: “given a market price, what’s the true probability?” They want to combine a bunch of sportsbooks to reach a fair number, then use it to beat whatever bookie they’re up against. A legitimate idea, but not the one we’ll investigate in this passage. Instead, we’ll have a look at a much less analyzed one, the inverse question. It’s interesting on its own, and, as noted above, it’ll most likely help us understand the reverse one better.
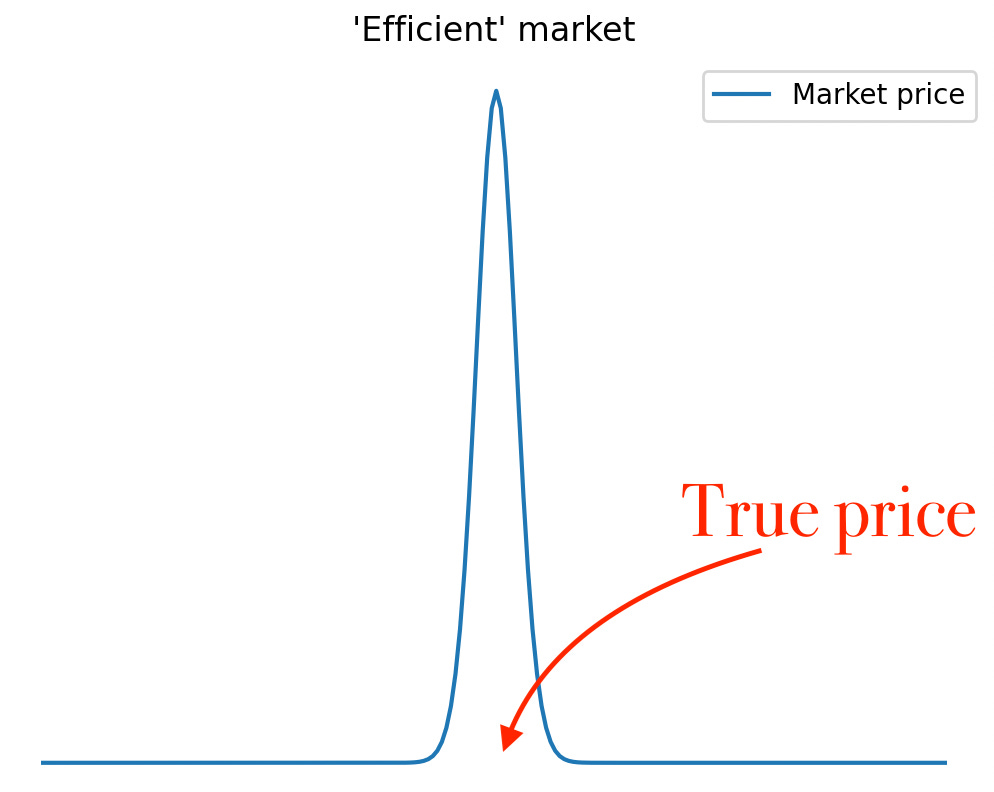
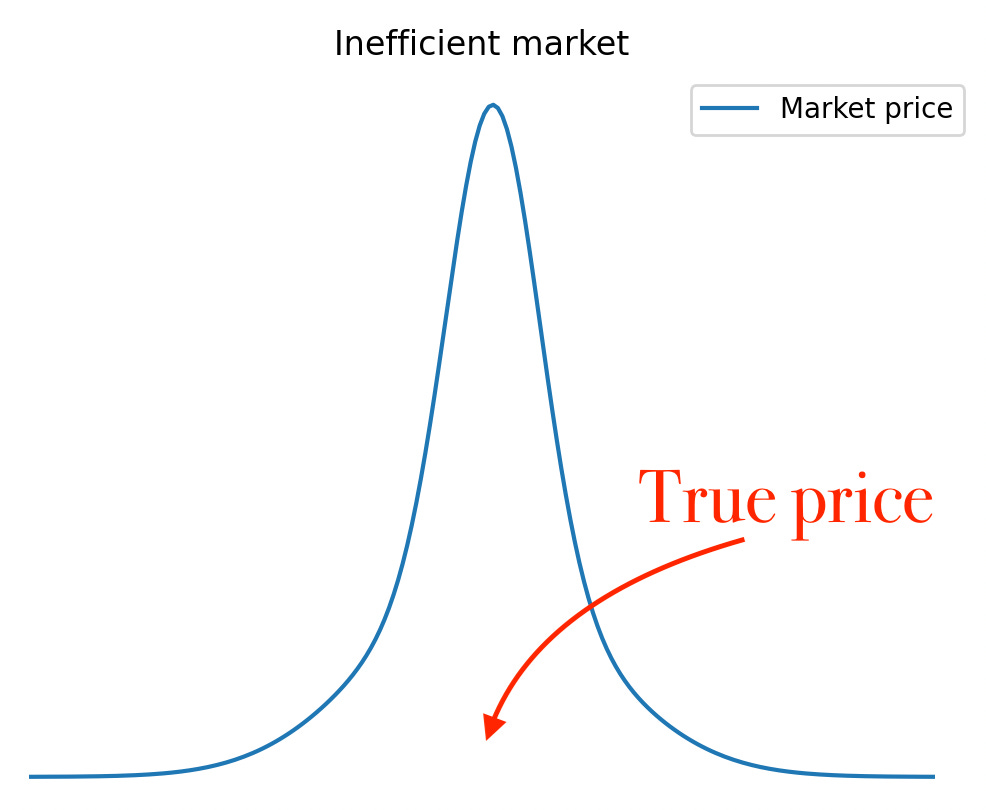
Q: “Given a true, underlying probability [e.g. a horse winning a race], what does the probability distribution of the market price look like?”
The answer to this question is the ultimate & only *real* measure of market efficiency.
In an efficient market, the distribution must collapse at the true price.
In an inefficient one, the price distribution might either be biased or spread out, or both.
& different degrees of market efficiency are perfectly incorporated in this model simply by varying the shape of the distribution.
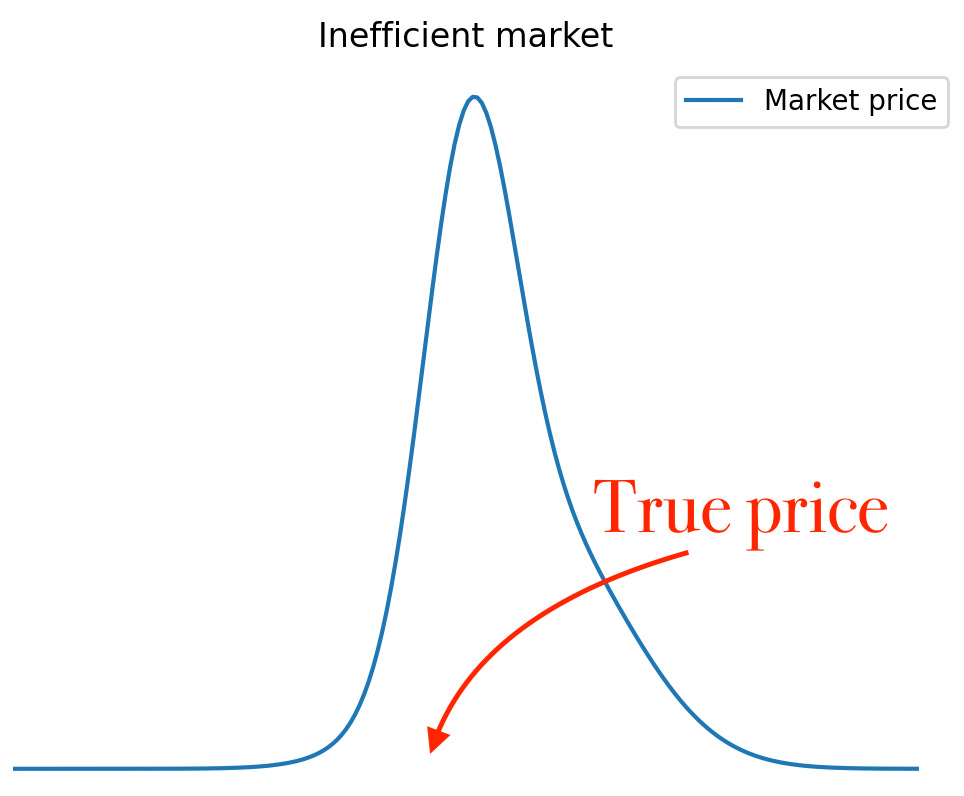
Note: In general there is no need to come up with parameters & plots. Close your eyes and visualize the distributions instead. Mind > Python. & if what you see is a normal distribution, NGMI… ;)
Now, having developed this distributional market efficiency framework, we’re ready to have a look at the problem with standard market efficiency studies. The ordinary reasoning goes somewhat like this:
Collect historical data on closing prices.
Sort them into different price buckets, odds in [1.00, 1.20], (1.20, 1.50], (1.50, 2.00] and so on.
For each price bucket, compute the fraction of wins for the observed data points.
Note that this fraction lies close to the implied probability & conclude market efficiency.
Since, as established before, market efficiency cannot be practically proven, and any attempt at doing so will inevitably crumble, we now find ourselves compelled to uncover the erroneous reasoning within this argument.
Having spent many hours in Bayes Boot Camp, we see it at first glance.
There are a ton of alternative realities [wherein markets are assumed to be inefficient] that could have generated the same data.
A common application of Bayes is to update your beliefs regarding different, alternative realities as you observe new evidence. Thus, you get used to asking yourself: what alternative frameworks could have generated the data I’m seeing? Unless there’s only one such framework, you can never, ever conclude anything simply by observing the new piece of information. All you can do is to reweight your probabilities/beliefs regarding the different scenarios.
The problem here [& definitely not only here, see this all the time]: a complete failure to consider any alternative realities. Yes, if markets *were* efficient, then you would expect to see this data. But that does in no way imply the reverse, i.e. that if you see this data, then markets must be efficient. Why? Because even if markets aren’t efficient, there may still be many ways for this data to be seen, and unless you have successfully disproven *all* such situations, you really haven’t proven anything & you definitely cannot conclude that your framework is correct.
Taleb believes all swans are white.
The next day he sees another white swan.
Taleb is now certain all swans are white.
…
A bookmaker prices all NBA games during a full season at even odds, i.e. 2.00 for the home team, 2.00 for the away team. At the end of the season, his data analytics team comes up to him & reveals that his pricing has indeed been very efficient. The 2.00/50 % outcomes won half of the time! Yet he’s infinitely poor.
Onto the second bookmaker! When this dude puts up an odds of 10.00, the outcome is equally likely to possess a true probability of either 5 or 15 %. In hindsight, again, his pricing is very sharp since his 10.00 horses wins a tenth of the time. The problem? Also this bookie is infinitely poor.
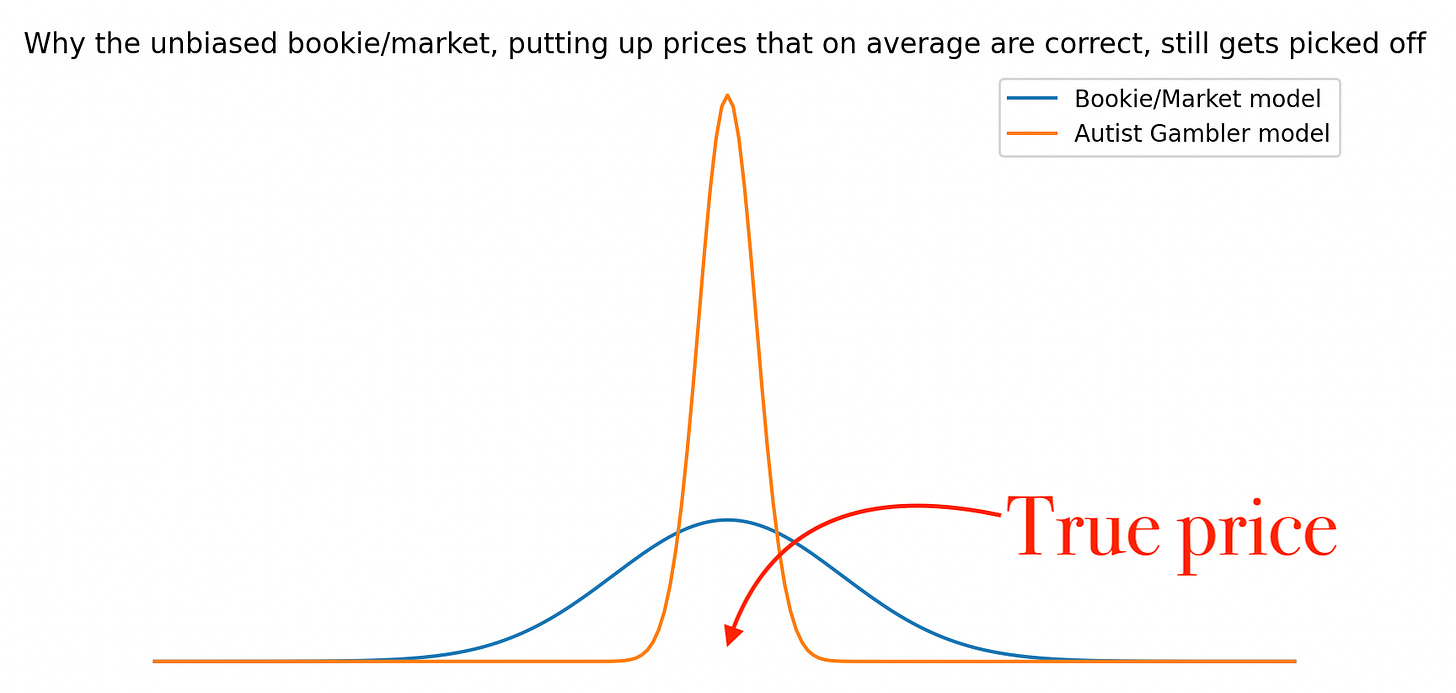
The third bookie [well, the real bookie] possesses an odds/probability distribution that is centered at the fair odds [unbiased], but with some spread around it. His 10.00 horses are as likely to be a 8 % horse as a 12 % horse & so on. He rarely misses by a huge margin, but there’s still some wiggle-room when he puts up a price. Again, “market efficiency”. Again, a negative result at the end of the year.
Do you see it yet?
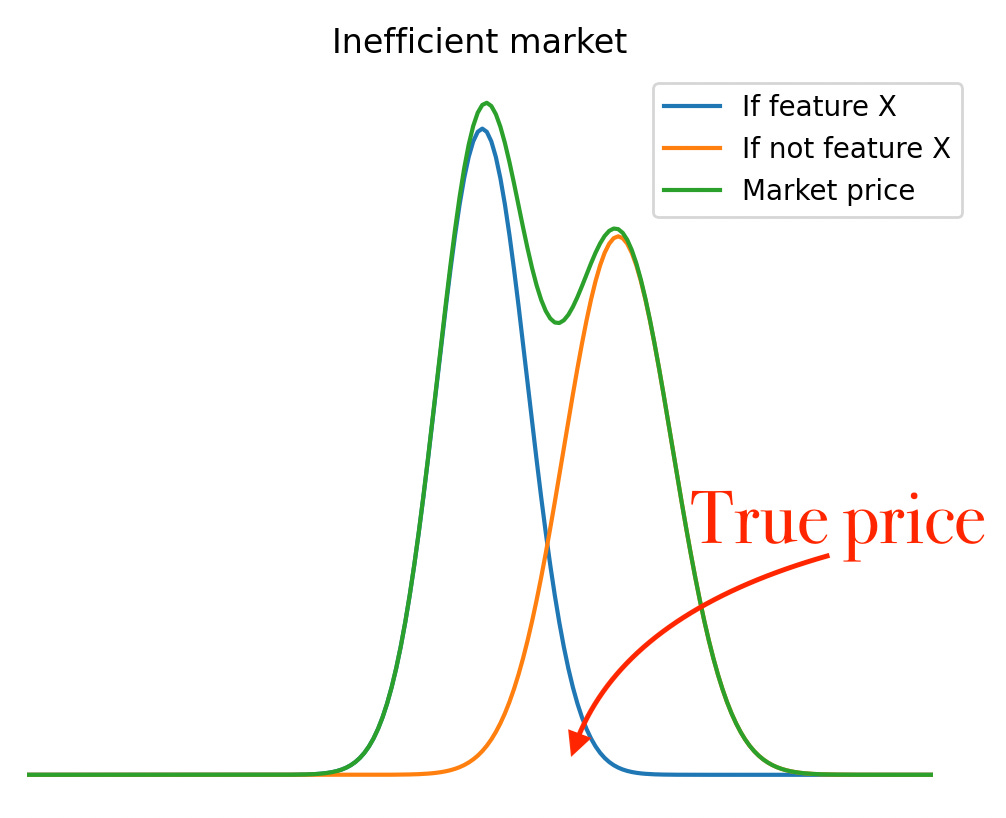
This relates to another phenomenon: in previous posts & in many Bird App tweets we’ve repeatedly been saying the following: "If you have *more information* than your counterparty, you’ll always end up taking his/her money over time” [at least as a bettor/price taker].
Having come this far in our distributional thinking, we’re now ready to see why [a picture tells more than a thousand words…].
Note: Information ≠ data. Information = data + ability to process data.
Question for Plato: Under what circumstances will the Autist Gambler in the picture above place a bet with the market/bookie?
Note: A bookie & a market can in many cases be different names of the same thing. Hint: What makes the bookie adjust his odds?
This post has been yet another proof that people waste too much time thinking about averages [IYKYK].
Final note: Some of our arguments in this post haven’t been perfected yet. If you can see why, congratulations on being an absolute turbo!
Until next time…
Disclaimer: None of this is to be deemed legal or financial advice of any kind. These are *opinions* written by an anonymous group of mathematicians who moved into betting.





Very insightful, thannk you. A brief question, though. How could you know what the true prob is, in order to find wrong odds?